【Three.js】ベクトルの内積を表示するアニメーション

どうもです、タドスケです。
しぬまでワクワクしていたい
【Three.js】Canvas 上で 3D行列計算結果を確認するサンプル | しぬまでワクワクしていたい
どうもです、タドスケです。 最近、仕事で行列計算のコードに触る機会が出てきました。 しかし僕は日頃から公言しているとおり、物理数学が大の苦手なゲームプログラマーで…
こちらの記事で、Three.js を使ってブログ記事上で軽量な 3D コンテンツを扱えることを知りました。
前回は行列計算をやったので、今回はベクトルを使ってみました。

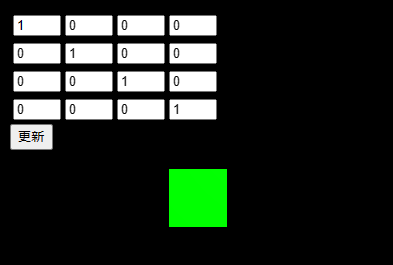
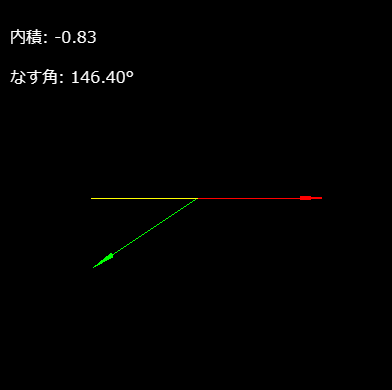








コメント
コメント一覧 (1件)
[…] […]